下是结合图文说明的 PID 控制算法与整定算法内容,通过示意图和流程图帮助理解核心概念:
PID 控制算法与整定算法
一、PID 控制算法的基本原理
PID 控制器通过比例(P)、积分(I)、微分(D)三个环节的协同,根据偏差信号(设定值与实际值的差值)输出控制量,实现对被控对象的精准控制。
1. PID 控制系统结构示意图
plaintext
设定值 r(t) ──┐ │ ▼ 偏差 e(t) = r(t) - y(t) → [PID控制器] → 控制量 u(t) → [被控对象] → 输出 y(t) ▲ │ └──────────────────────────────────────┘ 反馈回路
- 核心公式(连续时间域):\(u(t) = K_p \left[ e(t) + \frac{1}{T_i} \int_0^t e(\tau) d\tau + T_d \frac{de(t)}{dt} \right]\)
2. 各环节作用及响应曲线对比
通过 “水温控制” 案例理解三环节的差异(设定水温为 50℃,初始水温 20℃):
| 环节 | 作用示意图 | 核心特点 |
|---|---|---|
| 比例(P) | 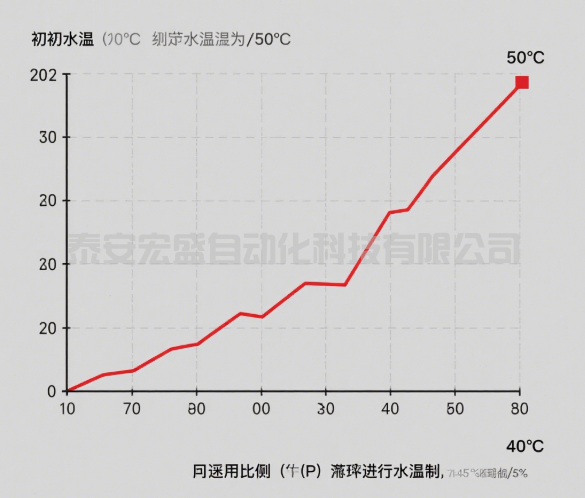 | - 响应快,偏差越大,加热越强; - 存在稳态误差(余差),无法精准达到设定值。 |
| 比例 + 积分(PI) | 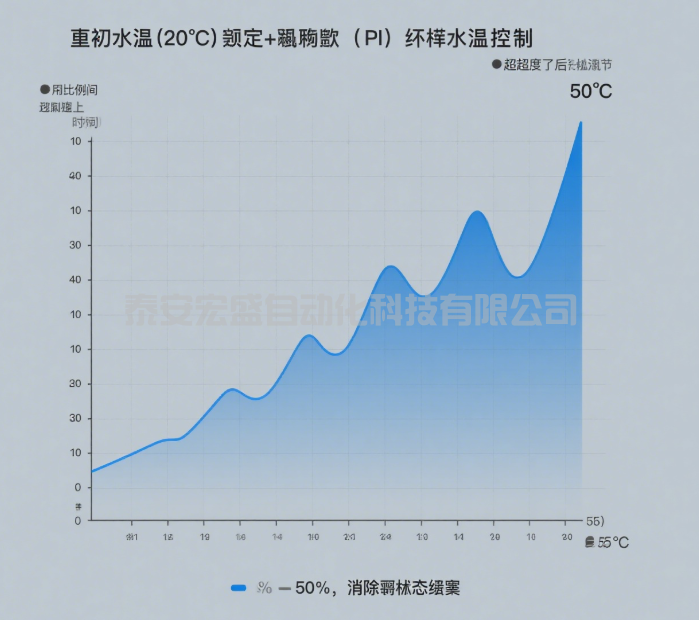 | - 积分作用消除稳态误差; - 可能出现超调(控制量 “冲过头”)。 |
| 比例 + 积分 + 微分(PID) | 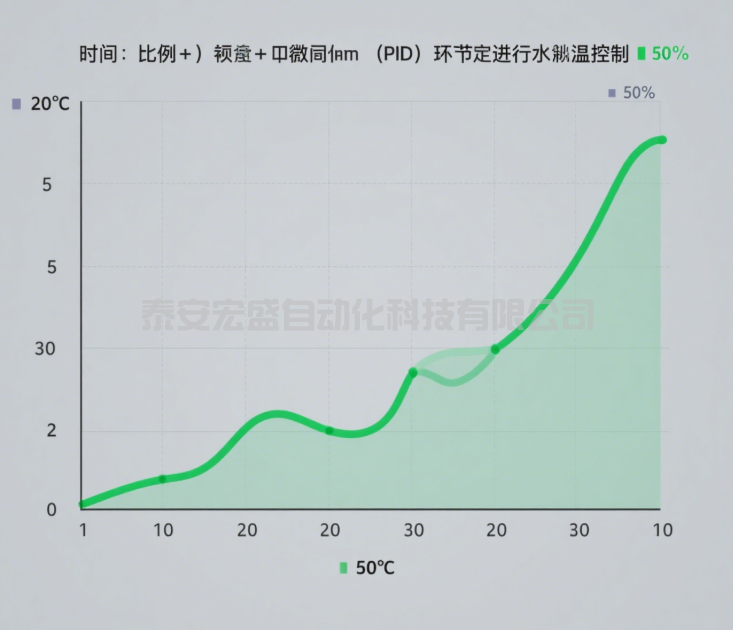 | - 微分环节提前抑制超调,响应更平稳; - 兼顾快速性与稳定性。 |
二、PID 参数整定算法
整定的目标是确定\(K_p\)、\(T_i\)、\(T_d\),使系统满足 “超调小、调节快、无余差”。以下为常见方法的流程图与说明:
1. 临界比例度法(Ziegler-Nichols 法之一)
适用场景:允许短期震荡的系统(如普通工业加热设备)。整定流程:
plaintext
开始 → 关闭I(T_i=∞)和D(T_d=0)→ 系统闭环运行 → 逐步增大K_p,直到阶跃响应出现等幅震荡(临界状态) → 记录临界参数:临界比例系数K_pcr、临界周期Tcr → 按经验公式计算PID参数: - P控制器:K_p = 0.5K_pcr - PI控制器:K_p=0.45K_pcr,T_i=0.85Tcr - PID控制器:K_p=0.6K_pcr,T_i=0.5Tcr,T_d=0.125Tcr → 测试响应,微调参数 → 结束
临界震荡示意图:
plaintext
输出y(t) ↑ | ┌───┐ ┌───┐ | / \ / \ | / \_/ \_ ...(等幅震荡) | / | / |─┘─────────────────────── 设定值r(t) └───────────────────→ 时间t
2. 阶跃响应法(开环整定)
适用场景:不允许震荡的系统(如精密仪器温度控制)。核心步骤:
- 开环状态下,对被控对象施加阶跃输入,记录输出的 “S 型曲线”:plaintext
输出y(t) ↑ | ┌─── 稳态值 | / | / | / | / |/ |───────────┐────────→ 时间t 阶跃输入开始 (L:纯滞后时间,T:时间常数)
- 根据曲线提取L(纯滞后时间)和T(时间常数),按公式计算参数(如\(K_p=1.2T/L\),\(T_i=2L\),\(T_d=0.5L\))。
3. 衰减曲线法
适用场景:对稳定性要求高的系统(如化工反应釜)。核心思路:通过调整\(K_p\)使系统响应达到4:1 衰减比(第一次超调量:第二次超调量 = 4:1),再计算参数。4:1 衰减响应示意图:
plaintext
输出y(t) ↑ | 第一次超调(A) | ┌───┐ | / \ 第二次超调(B) | / \_/ |/ |─────────────────── 设定值r(t) | A:B = 4:1 └────────────────→ 时间t
4. 智能整定法(以模糊整定为例)
适用场景:非线性、时变系统(如机器人关节控制)。核心逻辑:通过模糊规则动态调整参数,例如:
- 若 “偏差大且快速增大”→ 减小\(K_p\),增大\(T_d\)(抑制超调);
- 若 “偏差小且趋于稳定”→ 增大\(T_i\)(减弱积分,避免震荡)。
三、参数调整口诀与效果对应表
| 系统问题 | 调整方向(P/I/D) | 示意图(响应变化) |
|---|---|---|
| 稳态误差大(余差) | 减小\(T_i\)(增强积分) | 余差逐渐消除,最终稳定在设定值 |
| 超调量大、震荡剧烈 | 减小\(K_p\)或增大\(T_d\) | 超调幅度降低,震荡次数减少 |
| 响应速度慢 | 增大\(K_p\)或减小\(T_i\) | 达到设定值的时间缩短 |
| 对噪声敏感(输出波动) | 减小\(T_d\)(减弱微分) | 输出曲线更平滑,噪声干扰被抑制 |
通过以上图文结合的方式,可以更直观地理解 PID 控制的原理和整定逻辑。实际应用中,需根据被控对象的特性(如惯性、滞后)选择合适的整定方法,并通过多次测试微调参数。



